机器人的控制方法，根据控制量、控制算法的不同分为多种类型。下面分别针对不同的类型，介绍常用的机器人控制方法。

一、根据控制量分类

       按照控制量所处空间的不同，机器人控制可以分为关节空间的控制和笛卡尔空间的控制。对于串联式多关节机器人，关节空间的控制是针对机器人各个关节的变量进行的控制，笛卡尔空间控制是针对机器人末端的变量进行的控制。按照控制量的不同，机器人控制可以分为：位置控制、速度控制、加速度控制、力控制、力位混合控制等。这些控制可以是关节空间的控制，也可以是末端笛卡尔空间的控制。

       位置控制的目标是使被控机器人的关节或末端达到期望的位置。下面以关节空间位置控制为例，说明机器人的位置控制。如图1-1所示，关节位置给定值与当前值比较得到的误差作为位置控制器的输入量，经过位置控制器的运算后，其输出作为关节速度控制的给定值。关节位置控制器常采用PID算法，也可以采用模糊控制算法。

图1-1 关节位置控制示意图

       在图1-1中，去掉位置外环，即为机器人的关节速度控制框图。通常，在目标跟踪任务中，采用机器人的速度控制。此外，对于机器人末端笛卡尔空间的位置、速度控制，其基本原理与关节空间的位置和速度控制类似。

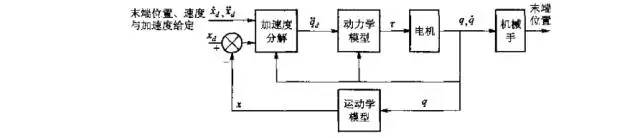
图1-2 加速度控制示意图

       图1-2所示为分解加速度运动控制示意图。首先，计算出末端工具的控制加速度。然后，根据末端的位置，速度和加速度期望值，以及当前的末端位置、关节位置与速度，分解出各关节相应的加速度，再利用动力学方程计算出控制力矩分解加速度控制，需要针对各个关节进行力矩控制。

图1-3 关节力/力矩控制示意图

       图1-3为关节的力/力矩控制框图。由于关节力/力矩不易直接测量，而关节电机的电流又能够较好的反映关节电机的力矩，所以常采用关节电机的电流表示当前关节力/力矩的测量值。力控制器根据力/力矩的期望值与测量值之间的偏差，控制关节电机，使之表现出期望的力/力矩特性。

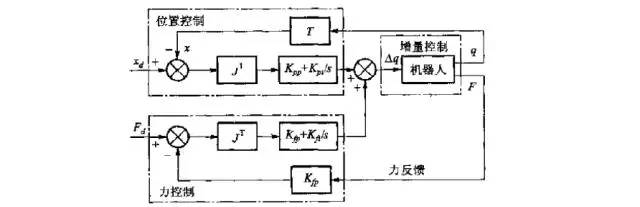
图1-4 力位混合控制框图

       图1-4所示为一种力位混合控制的框图，它由位置控制和力控制两部分组成。位置控制为PI控制，给定为机器人末端的笛卡尔空间位置，末端的笛卡尔空间位置反馈由关节空间的位置经过运动学计算得到。图中，T为机器人的运动学模型，J为机器人的雅克比矩阵。末端位置的给定值与当前值之差，利用雅克比矩阵的逆矩阵转换为关节空间的位置增量，再经过PI运算后，作为关节位置增量的一部分。

       力控制同样为PI控制，给定为机器人末端的笛卡尔空间力/力矩，反馈由力/力矩传感器测量获得。末端力/力矩的给定值与当前值之差，利用雅克比矩阵的转置矩阵转换为关节空间的力/力矩。关节空间的力/力矩经过PI运算后，作为关节位置增量的另一部分。位置控制部分和力控制部分的输出，相加后作为机器人关节的位置增量期望值。机器人利用增量控制，对其各个关节的位置进行控制。图1-5所示的力位混合控制，只是力位混合控制中的一种简单方案，是R-C（Raibert-Craig）力位混合控制的简化形式，在实际应用中应针对具体环境进行一些必要的修正。

二、根据控制算法分类

       按照控制算法的不同，机器人的控制方法可以分为PID控制、变结构控制、

       自适应控制、模糊控制、神经元网络控制等方法。也有的文献将现有的控制算法分为逻辑门限控制、PID控制、滑模变结构控制、神经网络控制和模糊控制等。这些控制方法并非孤立的，在一个控制系统之中常常结合在一起使用。

1、PID控制

       在工程实际中，应用最为广泛的调节器控制规律为比例、积分、微分控制，简称PID控制，又称PID调节。PID控制器问世至今已有近70年历史，它以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制的主要技术之一。当被控对象的结构和参数不能完全掌握，或得不到精确的数学模型时，控制理论的其它技术难以采用时，系统控制器的结构和参数必须依靠经验和现场调试来确定，这时应用PID控制技术最为方便。

       即当我们不完全了解一个系统和被控对象，或不能通过有效的测量手段来获得系统参数时，最适合用PID控制技术。PID控制，实际中也有PI和PD控制。PID控制器就是根据系统的误差，利用比例、积分、微分计算出控制量进行控制的。

2、变结构控制

       变结构控制是20世纪50年代从苏联发展起来的一种控制方案。所谓变结构控制，是指控制系统中具有多个控制器，根据一定的规则在不同的情况下采用不同的控制器。采用变结构控制具有许多其他控制所没有的优点，可以实现对一类具有不确定参数的非线性系统的控制。

3、自适应控制

       所谓自适应控制，是指系统的输入或干扰发生大范围的变化时，所设计的系统能够自适应调节系统参数或控制策略，使输出仍能达到设计的要求，其基本结构如图2-1所示。自适应控制所处理的是具有“不确定性”的系统，通过对随机变量状态的观测和系统模型的辨识，设法降低这种不确定性。控制结果常常是达到一定的控制指标，即“最优的控制”被“有效的控制”所取代。

       自适应控制系统按其原理的不同，可分为模型参考自适应控制系统、自校正控制系统、自寻优控制系统、变结构控制系统和智能自适应控制系统等。在这些类型的自适应控制系统中，模型参考自适应控制系统和自校正控制系统较成熟，也较常用。

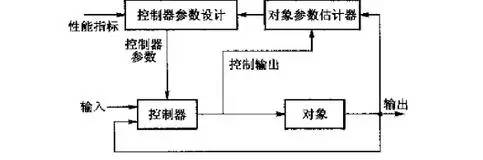
图2-1 自校正控制系统的基本结构

4、模糊控制

       在模糊控制中，输入量经过模糊量化成为模糊变量，有模糊变量经过模糊规则的推理获得模糊输出，经过解模糊得到清晰的输出量用于控制。模糊控制最早

       在1965年由美国加利福尼亚大学的Zadeh教授提出，1974年英国的E.H.Mamdani成功地将模糊控制应用于锅炉和蒸汽机控制。随后，模糊控制在控制领域得到了快速发展，并获得大量成功的应用。

5、神经元网络控制

       神经网络控制是20世纪80年代末期发展起来的自动控制领域的前沿学科之一。它是智能控制的一个新的分支，为解决复杂的非线性、不确定、不确知系统的控制问题开辟了新途径。 神经网络控制是（人工）神经网络理论与控制理论相结合的产物，是发展中的学科。它汇集了包括数学、生物学、神经生理学、脑科学、遗传学、人工智能、计算机科学、自动控制等学科的理论、技术、方法及研究成果，其基本结构如图2-2所示。

       在控制领域，将具有学习能力的控制系统称为学习控制系统，属于智能控制系统。神经控制是有学习能力的，属于学习控制，是智能控制的一个分支。 神经控制发展至今，虽仅有十余年的历史，已有了多种控制结构。如神经预测控制、神经逆系统控制等。

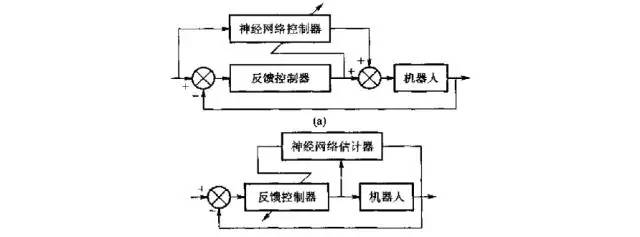
图2-2 神经网络控制系统结构